In this talk, we consider the second-order differential equation
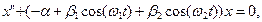 (1)
(1)
where α, βi and ωi (i = 1,2) are real numbers, ω1 > 0 and ω2 > 0. This equation is referred to as Mathieu's equation when ω1 = 2 and β2 = 0. If ω1/ω2 is irrational number, then the coefficient is not periodic. In such a case, our equation has been called a quasi-periodic Mathieu equation. The purpose of this talk is to give conditions which guarantee that all non-trivial solutions of (1) are nonoscillatory.
Kazuki Ishibashi,Shimane University博士研究生(导师Jitsuro Sugie教授)。2013年在Okayama University of Science获得学士学位,2015年在Shimane University获硕士学位。曾于2015年4-9月在我校交流学习。主要从事微分方程振动性研究,在J. Math. Anal. Appl.发表研究论文一篇。