This talk deals with the chemotaxis system for the couple tumor invasion

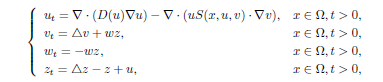
in a smooth bounded domain 2 Rn(n = 1; 2; 3; 4; 5), subject to the nonnegative initial data and homogeneous Neumann boundary conditions, where D is a given function satisfying D(u) CDum􀀀1 for all u > 0 with m > 0 and CD > 0. S is a given function with values in Rn nwhich ful lls jS(x; u; v)j CS(1 + u)􀀀 with some CS > 0 and > 0. It is shown that for any nonnegative and suitably regular initial data, this system possesses a unique global bounded classical solution under some assumptions. Based on the boundedness property, it can nally be proved that the above solutions approach to the spatially homogenous equilibrium in the sense that stabilizes to the constant stationary solution in an appropriate sense.